Wyprowadzenie wzorów użytych w modelu matematycznym kalkulatora

Opis kalkulatora torpedowego nie zawiera – ze względu na czytelność - szczegółowego wyprowadzenia wszystkich wzorów. Przekształcenia tych wzorów przedstawione zostały poniżej.

Przekształcenie wzoru na kąt strzału torpedowego

Przekształćmy wzór:

\[\begin{aligned} sin β = \frac{v_{g}}{v_{t}} * sin γ \end{aligned} \]

tak aby kąt strzału torpedy β był funkcją kąta uderzenia torpedy α oraz ilorazu \(\frac{v_{g}}{v_{t}} \).

Ponieważ jedną z wartości wejściowych bloku rozwiązywania trójkąta torpedowego jest iloraz \(\frac{v_{g}}{v_{t}} \), dokonujemy następującego podstawienia:

\[\begin{aligned} u = \frac{v_{g}}{v_{t}} \end{aligned} \]

otrzymując:

\[\begin{aligned} sin β = u * sin γ \end{aligned} \]

Ponieważ w trójkącie suma wszystkich kątów jest zawsze równa 180°, zatem można zapisać:

\[\begin{aligned} γ = 180° - (α + β) \end{aligned} \]

Uwzględniając okresowość funkcji sinus – czyli własność, że 

\[\begin{aligned} sin α = sin (180° - α) \end{aligned} \]

otrzymujemy:

\[\begin{aligned} sin γ = sin (α + β) \end{aligned} \]

Zatem ostatecznie możemy zapisać:

\[\begin{aligned} sin β = u * sin (α + β) \end{aligned} \]

Wzór ten można dalej przekształcić następująco:

\[\begin{aligned} sin β = u * (sin α * cos β + cos α * sin β) \end{aligned} \]

\[\begin{aligned} 1 = u * \frac{(sin α * cos β + cos α * sin β)}{sin β} \end{aligned} \]

\[\begin{aligned} 1 = u * (sin α * ctg β + cos α) \end{aligned} \]

\[\begin{aligned} 1 - u * cos α = u * sin α * ctg β \end{aligned} \]

\[\begin{aligned} ctg β = \frac{1 - u * cos α}{u * sin α} = \frac{1}{u * sin α} - ctg α \end{aligned} \]

Zatem kąt strzału torpedowego β mógł być wyznaczony przy znajomości ilorazu prędkości celu i torpedy oraz po wprowadzeniu kąta uderzenia torpedy przy użyciu następującej formuły:

\[\begin{aligned} β = arcctg (\frac{1}{u * sin α} - ctg α \end{aligned}) \]

Wyprowadzenie wzoru na współrzędne kartezjańskie punktu idealnego strzału torpedy

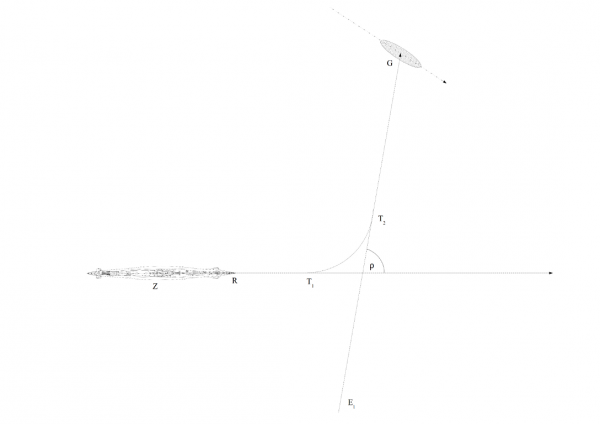
Tor biegu torpedy składa się z trzech części: początkowego prostoliniowego odcinka RT₁,  łuku T₁T₂, po którym torpeda wchodzi na swój ostateczny kurs, oraz odcinka T₂G, stanowiącego ostateczny tor biegu torpedy do momentu trafienia w cel.

Rysunek 1

Punkt idealnego strzału torpedy E₁ znajduje się na prostej pokrywającej się z ostatecznym torem biegu torpedy. Znajduje się on w odległości |E₁T₂| równej sumie długości łuku T₁T₂ oraz długości odcinka RT₁. Długość odcinka |RT₁| jest stała i dla niemieckich torped była równa 9,5 metra. Długość łuku |T₁T₂| zależała od wartości kąta odchylenia żyroskopowego ρ.

Współrzędne kartezjańskie x₀ i y₀ punktu idealnego strzału torpedy E₁ względem miejsca lokalizacji celownika Z (którego odległość od wyrzutni torpedowych na okrętach typu VIIC wynosiła około 27 metrów) można wyznaczyć w następujący sposób:

Współrzędne x_r i y_r wyrzutni torpedowej R względem celownika Z wynoszą:

\[\begin{aligned} (x_{r}; y_{r}) = (27; 0) \end{aligned}\]

Współrzędne punktu T₁ względem celownika Z:

\[\begin{aligned} (x_{T1}; y_{T1}) = (x_{r}; y_{r}) + (9,5; 0) = (27; 0) + (9,5; 0) \end{aligned}\]

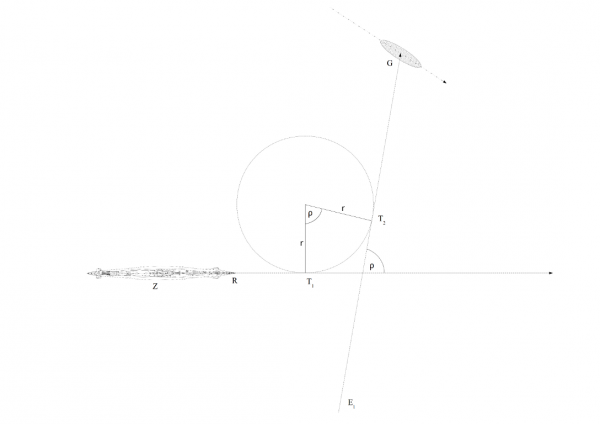
Położenie punktu T₂ (względem punktu T₁) można wyznaczyć z następującej zależności (zauważywszy, że kąt oparty na łuku T₁T₂ jest równy kątowi odchylenia żyroskopowego ρ):

\[\begin{aligned} (x_{T2}; y_{T2}) = (r * sin ρ; r – r * cos ρ) \end{aligned}\] 

gdzie r – promień skrętu, który dla niemieckich torped wynosił 95 metrów.

Natomiast względem celownika, współrzędne będą się równać:

\[\begin{aligned} (x_{T2}; y_{T2}) = (r * sin ρ; r – r * cos ρ) + (27; 0) + (9,5; 0) \end{aligned}\]

Rysunek 2

Długość łuku T₁T₂ wynosi 

\[\begin{aligned} |T_{1}T_{2}| = ρ * r \end{aligned}\]

gdzie kąt ρ jest wyrażony w radianach.

Jak wspomniano wcześniej, odległość pomiędzy punktem E₁ a punktem T₂ jest równa sumie:

\[\begin{aligned} |E_{1}T_{2}| = |RT_{1}| + |T_{1}T_{2}|  \end{aligned}\]

czyli

\[\begin{aligned} |E_{1}T_{2}| = 9,5 + ρ * r \end{aligned}\]

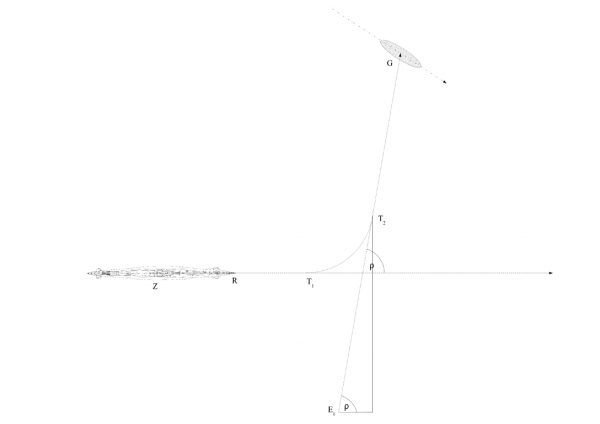
Współrzędne punktu E₁ względem punktu T₂ są równe:

\[\begin{aligned} (x_{E1}; y_{E1}) = (x_{T2}; y_{T2}) – (|E_{1}T_{2}| * cos ρ; |E_{1}T_{2}| * sin ρ) \end{aligned}\]

Rysunek 3

Współrzędne punktu E₁ względem celownika Z będą wynosić:

\[\begin{aligned} (x_{E1}; y_{E1}) = (r * sin ρ; r – r * cos ρ) + (27; 0) + (9,5; 0) – (|E_{1}T_{2}| * cos ρ; |E_{1}T_{2}| * sin ρ) \end{aligned}\]

Po wstawieniu zależności określającej długość odcinka |E₁T₂| otrzymujemy:

\[\begin{aligned} (x_{E1}; y_{E1}) = (r * sin ρ; r – r * cos ρ) + (27; 0) + (9,5; 0) – ((9,5 + ρ * r) * cos ρ; (9,5 + ρ * r )* sin ρ) \end{aligned}\]

Zatem współrzędne punktu E₁ wynoszą:

\[\begin{cases} x_{E1} = r * sin ρ  + 27 + 9,5 – (9,5 + ρ * r) * cos ρ \\ y_{E1} = r – r * cos ρ – (9,5 + ρ * r) * sin ρ \end{cases}\]

czyli

\[\begin{cases} x_{E1} = 27 + 9,5 + 95 * sin ρ  – (9,5 + ρ * 95) * cos ρ \\ y_{E1} = 95 * (1 – cos ρ) – (9,5 + ρ * 95) * sin ρ \end{cases}\]

Przekształcenie wzoru na kąt rozproszenia salwy torpedowej

Przekształcenie poniższego wzoru

\[\begin{aligned} \frac{E - λ * cos γ}{v_{t} * cos β + v_{g} * cos γ} = \frac{λ * sin γ}{v_{t} * sin β – v_{g} * sin γ} \end{aligned}\]

rozpoczynamy od dzielenia mianowników po obu stronach równania przez v_t otrzymując:

\[\begin{aligned} \frac{E - λ * cos γ}{cos β + \frac{v_{g}}{v_{t}} * cos γ} = \frac{λ * sin γ}{sin β – \frac{v_{g}}{v_{t}} * sin γ} \end{aligned}\]

Wykonując następujące podstawienie:

\[\begin{aligned} u = \frac{v_{g}}{v_{t}} \end{aligned}\]

otrzymujemy:

\[\begin{aligned} \frac{E - λ * cos γ}{cos β + u * cos γ} = \frac{λ * sin γ}{sin β – u * sin γ} \end{aligned}\] 

Dzieląc liczniki po obu stronach równania przez E otrzymujemy:

\[\begin{aligned} \frac{1 - \frac{λ}{E} * cos γ}{cos β + u * cos γ} = \frac{\frac{λ}{E} * sin γ}{sin β – u * sin γ} \end{aligned}\]

Wykonując następujące podstawienie:

\[\begin{aligned} μ = \frac{λ}{E} \end{aligned}\]

otrzymujemy:

\[\begin{aligned} \frac{1 - μ * cos γ}{cos β + u * cos γ} = \frac{μ * sin γ}{sin β – u * sin γ} \end{aligned}\]

Kolejne przekształcenia wyglądają następująco:

\[\begin{aligned} (1 - μ * cos γ)*(sin β – u * sin γ) = (μ * sin γ)*(cos β + u * cos γ) \end{aligned}\]

\[\begin{aligned} sin β - u * sin γ - μ * cos γ * sin β + μ * u * sin γ * cos γ = μ * sin γ * cos β + μ * u * sin γ * cos γ \end{aligned}\]

\[\begin{aligned} sin β - u * sin γ = μ * sin γ * cos β + μ * cos γ * sin β \end{aligned}\]

\[\begin{aligned} sin β - u * sin γ = μ * (sin γ * cos β + cos γ * sin β) \end{aligned}\]

otrzymując ostatecznie:

\[\begin{aligned} sin β - u * sin γ = μ * sin (γ + β) \end{aligned}\]

Jest to uwikłane równanie, które pozwala wyznaczyć kąt strzału torpedowego β dla celu widzianego pod kątem biegu γ, tak aby torpeda trafiła w punkt leżący w odległości λ od środka celu.

Dla wygody, zamiast rozpatrywać położenie rufy oraz dziobu celu jako odległości λ od środka celu, można wprowadzić następujące podstawienie:

\[\begin{aligned} μ_{0} = \frac{l}{2*E} \end{aligned}\]

gdzie l – długość celu.

Czyli aby trójtorpedowa salwa trafiła odpowiednio w dziób, środek oraz rufę celu o długości l, każda z trzech torped musi zostać wystrzelona pod kątem odpowiednio  β₀, β i β₁, gdzie każda z tych wartości spełnia jedno z następujących równań:

\[\begin{cases}sin β_{0} – u * sin γ = μ_{0} * sin (β_{0} + γ) \\ sin β – u * sin γ = 0  \\ sin β_{1} – u * sin γ = - μ_{0} * sin (β_{1} + γ)\end{cases}\]

Ponieważ w praktyce, w większości przypadków cel o długości do około 150 metrów (np. statki typu Liberty ~135 m, tankowce typu T2 ~152 m)  jest atakowany z odległości minimum 500 metrów, to wartość μ₀ jest niewielka (μ₀ < 0,15). Oznacza to, że kąt pomiędzy kursami torped trafiających w dziób i rufę celu (tzn.  β₁ - β₀) wynosi maksymalnie ~20º. Wykorzystując fakt, że dla kąta α z zakresu 0 – 20º, sin α ~  α oraz cos α ~ 1, można zapisać następujące równania:

\[\begin{align} sin β_{0} = sin (β_{0} - β + β) = sin (β_{0} - β) * cos β + cos (β_{0} - β) * sin β \end{align}\]

oraz

\[\begin{align}sin β_{1} = sin (β_{1} - β + β) = sin (β_{1} - β) * cos β + cos (β_{1} - β) * sin β \end{align}\]

Wykorzystując wspomnianą wcześniej własność funkcji sinus i cosinus dla małych kątów, powyższe równania można zapisać w następującej formie:

\[\begin{align} sin β_{0} = (β_{0} - β) * cos β + sin β \end{align}\]

oraz

\[\begin{align} sin β_{1} = (β_{1} - β) * cos β + sin β \end{align}\]

Wstawiając powyższe zależności do wcześniejszych równań otrzymujemy:

\[\begin{cases} (β_{0} - β) * cos β + sin β - u * sin γ = μ_{0} * sin (β_{0} + γ) \\ sin β - u * sin γ = 0 \\ (β_{1} - β) * cos β + sin β - u * sin γ = -μ_{0} * sin (β_{1} + γ) \end{cases}\]

oraz po kolejnym przekształceniu:

\[\begin{cases} sin β - u * sin γ = μ_{0} * sin (β_{0} + γ) - (β_{0} - β) * cos β \\ sin β - u * sin γ = 0 \\ sin β - u * sin γ = -μ_{0} * sin (β_{1} + γ) - (β_{1} - β) * cos β \end{cases}\]

Wstawiając środkowe równanie do dwóch pozostałych otrzymujemy:

\[\begin{cases} 0 = μ_{0} * sin (β_{0} + γ) - (β_{0} - β) * cos β \\ 0 = -μ_{0} * sin (β_{1} + γ) - (β_{1} - β) * cos β \end{cases}\]

Porównując obydwa równania stronami otrzymujemy zależność:

\[\begin{aligned} μ_{0} * sin (β_{0} + γ) - (β_{0} - β) * cos β = -μ_{0} * sin (β_{1} + γ) - (β_{1} - β) * cos β \end{aligned}\]

co po prostym przekształceniu prowadzi do:

\[\begin{aligned} β_{0} - β_{1} = μ_{0} * \frac{sin (β_{0} + γ) + sin (β_{1} + γ)}{cos β} \end{aligned}\] 

Jak wspomniano wcześniej, różnica wartości kątów β₁ - β₀  w praktyce wynosi maksymalnie 20º. Funkcję sinus dla argumentów z zakresu wynoszącego maksymalnie o 20º można dobrze przybliżyć funkcją liniową. W związku z tym można zapisać, że:

\[\begin{aligned} sin (β + γ) = \frac{sin (β_{0} + γ) + sin (β_{1} + γ)}{2} \end{aligned}\]

gdy 

\[\begin{aligned} β \approx \frac{β_{0} + β_{1}}{2} \end{aligned}\]

Zatem kąt rozproszenia salwy torpedowej ψ (będący różnicą kątów β₁ – β₀) można obliczyć przy użyciu następującej formuły:

\[\begin{aligned} ψ = 2 * μ_{0} * \frac{sin (β + γ)}{cos β} \end{aligned}\]

To równanie można następnie przekształcić następująco, aby wyeliminować zależność od kąta strzału torpedy β:

\[\begin{aligned} ψ = 2 * μ_{0} * \frac{sin (β + γ)}{cos β} = \frac{l}{E} * \frac{sin (β + γ)}{cos β} = \frac{l}{E} * \frac{sin β * cos γ + cos β * sin γ}{cos β}\end{aligned}\]

\[\begin{aligned} ψ = \frac{l}{E} * \bigg(\frac{sin β * cos γ}{cos β} + \frac{cos β * sin γ}{cos β}\bigg) = \frac{l}{E} * (tg β * cos γ + sin γ)\end{aligned}\]

\[\begin{aligned} ψ = \frac{l}{E} * sin γ * \bigg(\frac{tg β * cos γ}{sin γ} + 1\bigg) = \frac{l}{E} * sin γ * \bigg(\frac{cos γ}{ctg β * sin γ} + 1\bigg) \end{aligned}\]

\[\begin{aligned} ψ = \frac{l}{E} * sin γ * \bigg(\frac{cos γ}{\frac{cos β}{sin β} * sin γ} + 1\bigg) = \frac{l}{E} * sin γ * \bigg(\frac{cos γ}{\sqrt{\frac{cos^2 β}{sin^2 β} * sin^2 γ}} + 1\bigg) \end{aligned}\]

\[\begin{aligned} ψ = \frac{l}{E} * sin γ * \bigg(\frac{cos γ}{\sqrt{\frac{1 - sin^2 β}{sin^2 β} * sin^2 γ}} + 1\bigg) = \frac{l}{E} * sin γ * \bigg(\frac{cos γ}{\sqrt{\frac{sin^2 γ - sin^2 β * sin^2 γ}{sin^2 β}}} + 1\bigg) \end{aligned}\]

\[\begin{aligned} ψ = \frac{l}{E} * sin γ * \bigg(\frac{cos γ}{\sqrt{\frac{sin^2 γ}{sin^2 β} - \frac{sin^2 β * sin^2 γ}{sin^2 β}}} + 1\bigg) \end{aligned}\]

Ponieważ

\[\begin{aligned} \frac{sin γ}{sin β} = \frac{v_{t}}{v_{g}} \end{aligned}\]

można ostatecznie zapisać:

\[\begin{aligned} ψ = \frac{l}{E} * sin γ * \bigg(\frac{cos γ}{\sqrt{(\frac{v_{t}}{v_{g}})^2 - sin^2 γ}} + 1\bigg) \end{aligned}\]