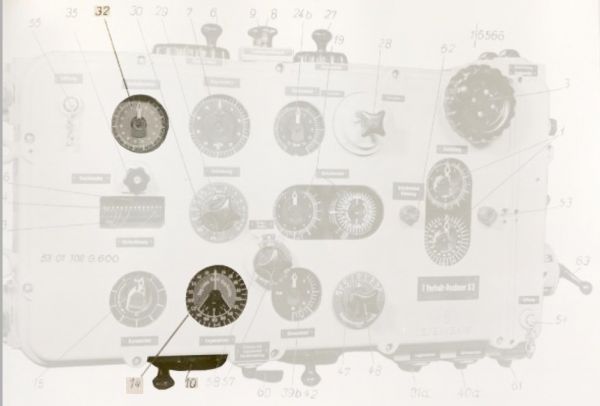
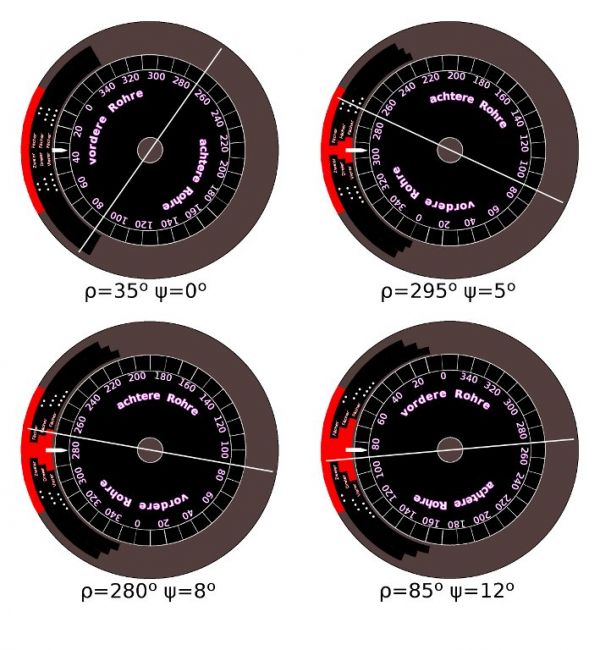
Kalkulator torpedowy T. Vh. Re. S3
Sercem systemu kierowania ogniem torpedowym był kalkulator torpedowy T. Vh. Re. S3 firmy Siemens. Było to elektromechaniczne urządzenie, którego zadaniem było rozwiązanie dwóch problemów:
- obliczenie kąta strzału torpedowego β oraz przeliczenie go na kąt odchylenia żyroskopowego ρ (z uwzględnieniem paralaksy δ wynikającej z różnego położenia celownika i wyrzutni torpedowej a także biorąc pod uwagę poprawkę wynikającą ze skrętu torpedy po opuszczeniu wyrzutni);
- obliczenie kąta rozproszenia salwy torpedowej ψ.
Prace nad konstrukcją tego urządzenia rozpoczęto około 1939 roku. W roku 1941 został (wraz z całym systemem kierowania ogniem torpedowym) oddany do testów prowadzonych przez Kriegsmarine. W tym samym roku – po pomyślnym ukończeniu testów – rozpoczęto jego instalację na U-Bootach.
Od roku 1941 - kiedy to kalkulator ten zaczął być używany - do końca wojny wprowadzono kilka modyfikacji jego konstrukcji.
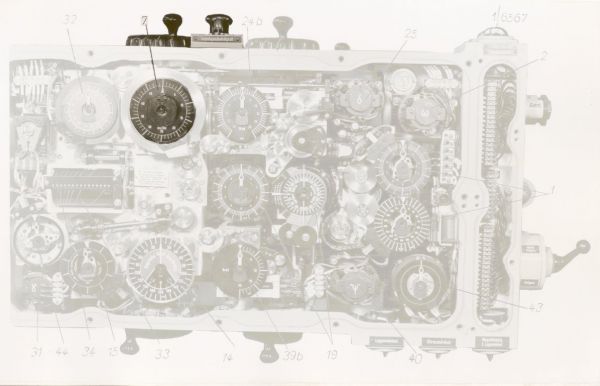
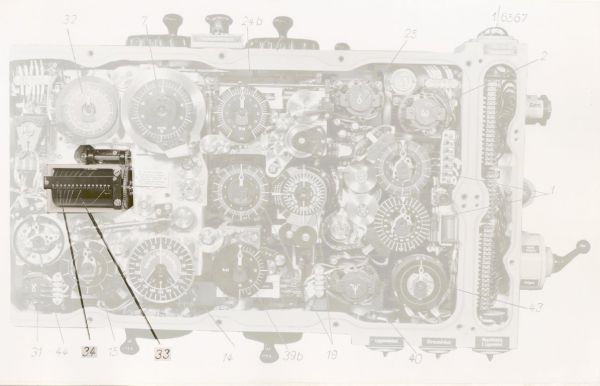
Fot. 1. Kalkulator torpedowy T. Vh. Re. S3 – wczesna wersja – widok pokrywy czołowej
Fot. 2. Kalkulator torpedowy T. Vh. Re. S3 – wczesna wersja – widok po zdjęciu pokrywy
Kalkulator mieścił się w metalowej obudowie o wymiarach około 106 cm x 45 cm x 13 cm. Był instalowany w kioskach okrętów podwodnych (za wyjątkiem okrętów typu II, gdzie z uwagi na niewielką ilość miejsca w kiosku instalowany był w centrali) - na sterburcie w przypadku okrętów typu VII oraz na bakburcie w przypadku okrętów typu IX i XXI. Na okrętach typu VII umieszczony był poziomo, natomiast na okrętach typu II, IX i XXI – pionowo.
W normalnym trybie działania, po wprowadzeniu przy pomocy pokręteł, parametrów ruchu celu, kalkulator (uwzględniając bieżący namiar na cel przekazywany z peryskopu/celownika nocnego UZO oraz kurs własny okrętu przekazywany z żyrokompasu) automatycznie obliczał rozwiązanie trójkąta strzału torpedowego oraz kąt rozproszenia salwy torpedowej. W przypadku uszkodzenia niektórych komponentów urządzenia lub awarii systemu elektrycznego, możliwa była całkowicie ręczna obsługa kalkulatora.
Kalkulator torpedowy funkcjonalnie składał się z kilku komponentów:
- bloku rozwiązywania trójkąta torpedowego;
- bloku obliczania poprawki paralaksy;
- bloku obliczania kąta odchylenia żyroskopowego;
- bloku obliczania maksymalnej odległości do celu w momencie odpalenia torpedy;
- bloku obliczania kąta rozproszenia salwy torpedowej;
- bloku wprowadzania kąta namiaru na cel;
- bloku obliczania bieżącego kąta biegu;
- bloku obliczania bieżącego namiaru na cel;
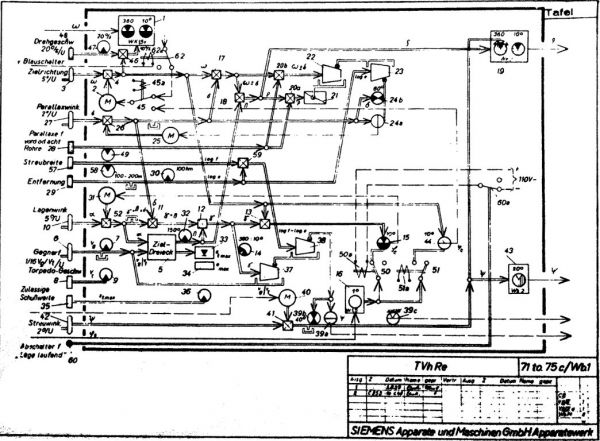
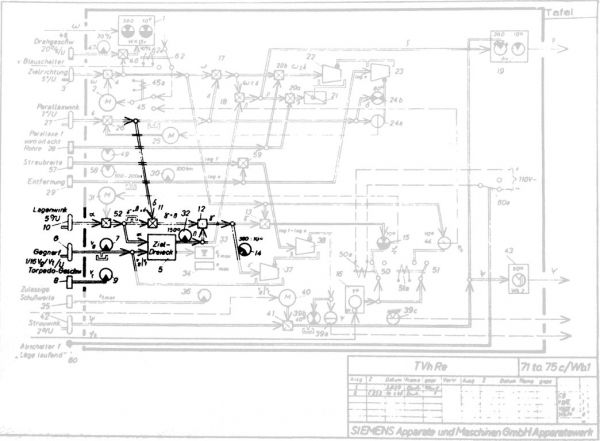
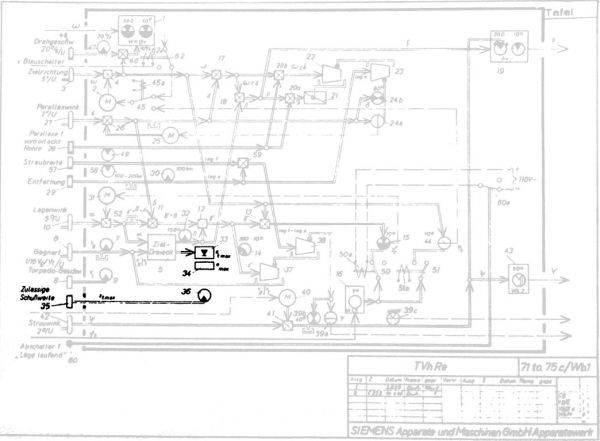
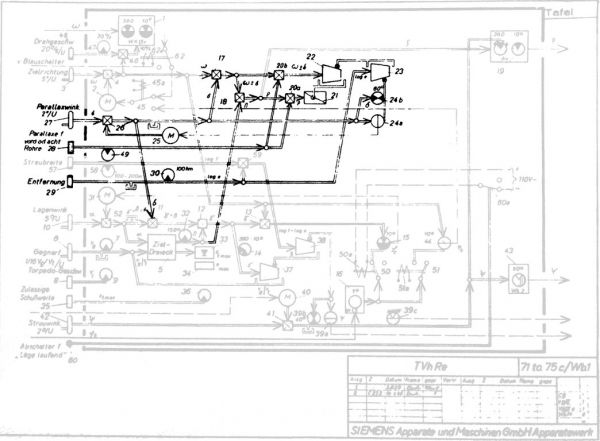
Rys. 1. Schemat kalkulatora torpedowego T. Vh. Re. S3 – stan na rok 1940 [1]
Opis bloku rozwiązywania trójkąta torpedowego:
Blok rozwiązywania trójkąta torpedowego na podstawie wprowadzonego kąta uderzenia torpedy α oraz ilorazu prędkości celu i prędkości torpedy \(\frac{v_{g}}{v_{t}} \) obliczał kąt strzału torpedy β. Dodatkowe wyjście z tego bloku dostarczało danych do bloku obliczenia maksymalnej odległości do celu w momencie odpalenia torpedy emax.
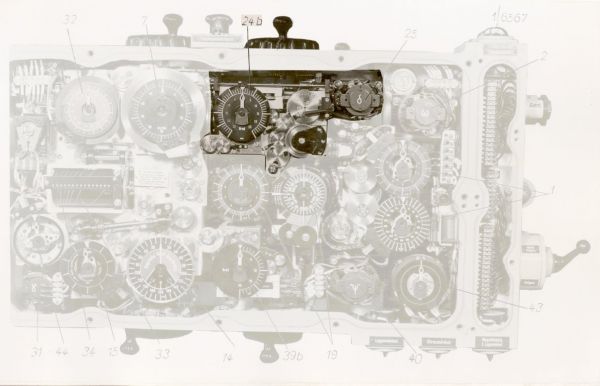
Fot. 3. Blok rozwiązywania trójkąta torpedowego – widok po zdjęciu pokrywy
(7) wskaźnik prędkości celu, (14) wskaźnik kąta biegu, (32) wskaźnik kąta strzału torpedy
Fot. 4. Blok rozwiązywania trójkąta torpedowego – widok pokrywy czołowej
(6) pokrętło prędkości celu, (7) wskaźnik prędkości celu, (8) pokrętło prędkości torpedy,
(9) wskaźnik prędkości torpedy, (14) wskaźnik kąta biegu, (32) wskaźnik kąta strzału torpedy
Do kalkulatora przy pomocy pokręteł wprowadzano prędkości torpedy vt oraz iloraz prędkości celu i torpedy \(\frac{v_{g}}{v_{t}} \).
We wczesnych wersjach kalkulatora, pokrętło prędkości torpedy mogło być ustawiane w trzech pozycjach (30, 40, 44 węzły – było to powodowane tym, że znajdujące się w użyciu torpedy parogazowe G7a posiadały możliwość nastawy prędkości na jedną z tych trzech wartości, a torpedy elektryczne G7e – mogły płynąć jedynie z prędkością 30 węzłów). Wartość ilorazu \(\frac{v_{g}}{v_{t}} \) oraz prędkość torpedy vt była wprowadzana do układu mnożącego (zrealizowanego w postaci układu z listwami zębatymi), w którym wyliczano wartość prędkości celu vg która wskazywana była na wskaźniku zegarowym. Po ustawieniu poprawnej prędkości torpedy, operator kręcąc pokrętłem ilorazu prędkości celu i torpedy doprowadzał do tego, że na wskaźniku prędkości celu wskazywana była poprawna wartość.
Dzięki takiemu rozwiązaniu uniknięto konieczności zastosowania stosunkowo złożonego układu do wyznaczania ilorazu na rzecz prostszego układu mnożącego.
W późniejszych wersjach kalkulatora prędkość celu oraz prędkość torpedy wskazywane były na zintegrowanym wskaźniku. Prędkość torpedy mogła być ustawiona na dowolną wartość z zakresu od 10 do 46 węzłów – było to związane z dostosowaniem kalkulatora do strzelania torpedami LUT oraz torpedami akustycznymi G7es.
Fot. 5. Pokrętła i wskaźniki prędkości celu oraz torpedy we wczesnej wersji kalkulatora
Fot. 6. Pokrętła i wskaźniki prędkości celu oraz torpedy w późnej wersji kalkulatora
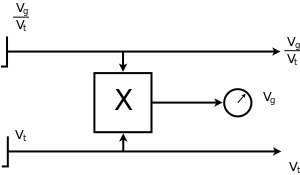
Rys. 2. Zasada wyznaczania ilorazu \(\frac{v_{g}}{v_{t}} \) we wczesnej wersji kalkulatora
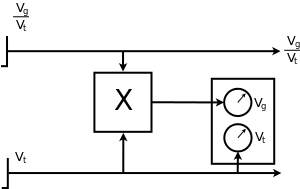
Rys. 3. Zasada wyznaczania ilorazu \(\frac{v_{g}}{v_{t}} \) w późnej wersji kalkulatora
Kąt biegu celu wprowadzany był pośrednio - przy pomocy pokrętła wprowadzano wartość kąta uderzenia torpedy α, która przekazywana była do bloku rozwiązywania trójkąta torpedowego. Kąt uderzenia torpedy α był jednocześnie sumowany z wartością kata strzału torpedy β (obliczonego na podstawie aktualnej wartości kąta uderzenia torpedy α oraz ilorazu prędkości celu oraz torpedy \(\frac{v_{g}}{v_{t}} \)) dając ostatecznie kąt biegu γ (wykorzystana tu została własność, że suma trzech kątów w trójkącie jest stała i wynosi 180°), który wskazywany był na wskaźniku zegarowym.
Rys. 4. Blok rozwiązywania trójkąta torpedowego [1]
Blok rozwiązywania trójkąta torpedowego wyznaczał kąt strzału torpedy β - czyli kąt pomiędzy linią namiaru na cel a torem biegu torpedy. Wartość tego kąta była wskazywana na wskaźniku zegarowym (o całkowitym zakresie 150°, ale w tarcza byłą podzielona po 75° na sterburtę i bakburtę).
Należy zwrócić uwagę, że w kalkulatorze torpedowym pochodzącym z U 955, tarcza tego wskaźnika ma zakres całkowity wynoszący 360°, (podzielony po 180° na sterburtę i bakburtę). Spowodowane jest to tym, że w późniejszych wersjach kalkulatora zrezygnowano z wizualizacji kąta strzału torpedy (Vorhaltwinkel) na rzecz wizualizacji kąta uderzenia torpedy (Scheidungswinkel).
Fot. 7. Pokrętło (10) i wskaźnik zegarowy (14) kąta biegu celu oraz wskaźnik (32) kąta strzału torpedy
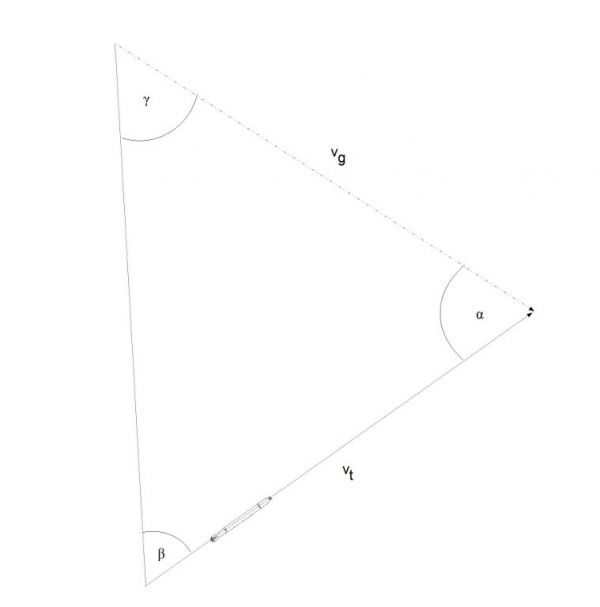
Trójkąt torpedowy ma postać jak na poniższym rysunku:
Rys. 5. Trójkąt torpedowy
Twierdzenie sinusów zastosowane do niego wygląda następująco:
\[\begin{aligned} \frac{v_{t}}{sin γ} = \frac{v_{g}}{sin β} \end{aligned} \]
czyli
\[\begin{aligned} sin β = sin γ * \frac{v_{g}}{v_{t}} \end{aligned} \]
Ze względu na to, że do bloku doprowadzana jest wartość ilorazu prędkości, można wykonać podstawienie:
\[\begin{aligned} u = \frac{v_{g}}{v_{t}} \end{aligned} \]
czyli
\[\begin{aligned} sin β = u * sin γ \end{aligned} \]
Ponieważ w trójkącie suma wszystkich kątów jest zawsze równa 180°, można zapisać:
\[\begin{aligned} γ = 180° - (α + β) \end{aligned} \]
czyli (ze względu na okresowość funkcji sinus)
\[\begin{aligned} sin γ = sin (α + β) \end{aligned} \]
Zatem otrzymujemy:
\[\begin{aligned} sin β = u * sin (α + β) \end{aligned}\]
co można przekształcić do ostatecznej postaci:
\[\begin{aligned} ctg β = \frac{1}{u * sin α} – ctg α \end{aligned} \]
Czyli kąt β strzału torpedowego był wyznaczony przy znajomości ilorazu prędkości celu i torpedy oraz po wprowadzeniu kąta uderzenia torpedy:
\[\begin{aligned} β = arc ctg (\frac{1}{u * sin α} – ctg α)\end{aligned}\]
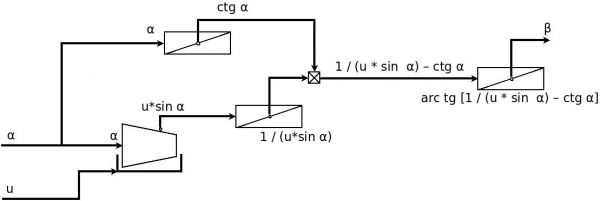
Fizycznie blok rozwiązywania trójkąta strzału torpedowego zaimplementowano najprawdopodobniej jako układ krzywek trójwymiarowych oraz mechanizmów różnicowych:
- krzywka dwuwymiarowa realizująca funkcję ctg α
- krzywka trójwymiarowa realizująca funkcję u * sin α
- dwuwymiarowa krzywka odwracająca wartość funkcji u * sin α
- mechanizm różnicowy wykonujący odejmowanie
- krzywka realizująca funkcję arc ctg
Rys. 6. Przypuszczalna implementacja bloku rozwiązywania trójkąta strzału torpedowego
Opis bloku obliczania poprawki paralaksy:
Blok rozwiązywania trójkąta strzału torpedowego modeluje idealną sytuację, w której celownik torpedowy znajduje się w tym samym miejscu co wyrzutnia torpedowa, a torpeda po opuszczeniu wyrzutni biegnie stałym kursem.
W przypadku okrętu podwodnego ta sytuacja oczywiście nie ma miejsca – celownik torpedowy znajduje się w pewnej odległości od wyrzutni torpedowych (dla U-Bootów typu VII – około 28 metrów). Oznacza to, że namiar na cel mierzony w miejscu wyrzutni torpedowej jest różny od namiaru na cel w miejscu celownika torpedowego. Podobnie jest z kątem biegu celu – obserwowany z miejsca celownika torpedowego ma inną wartość niż obserwowany z wyrzutni torpedowej.
Rys. 7. Różnica w namiarach oraz kątach biegu celu obserwowanych z miejsca lokalizacji celownika torpedowego oraz wyrzutni torpedowej
Ponadto, torpeda wykonując zwrot o kąt odchylenia żyroskopowego (po opuszczeniu wyrzutni) biegnie torem równoległym do linii łączącej wyrzutnię torpedową z punktem trafienia w cel – ale przesuniętym o wartość zależną od kąta odchylenia żyroskopowego ρ.
Rys. 8. Przesunięcie toru torpedy wynikające z wykonanego zwrotu
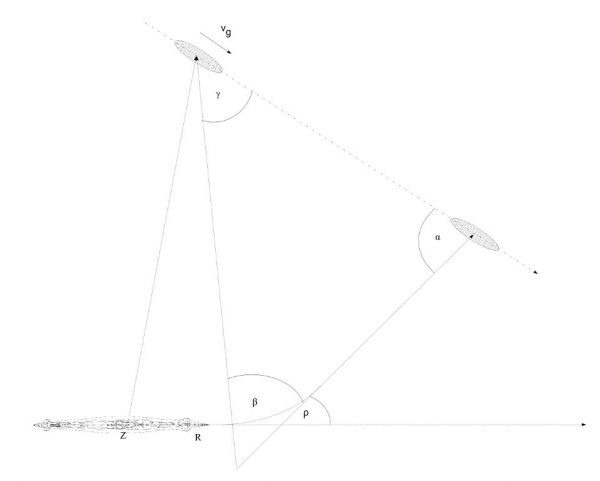
Obydwa te efekty wymagają wprowadzenia do trójkąta torpedowego pewnej poprawki kątowej, zwanej poprawką paralaksy δ (niem. Winkelparalaxverbesserung, ang. paralax correction). Trójkąt torpedowy uwzględniający poprawkę paralaksy zbudowany był w oparciu o tzw. idealny punkt startu torpedy (niem. ideeller Torpedoeintrittsort, ang. equivalent point of fire).
Rys. 9. Trójkąt torpedowy uwzględniający paralaksę w oparciu o idealny punkt strzału torpedy
Idealny punkt startu torpedy znajduje się na przedłużeniu toru torpedy, w odległości równej sumie długości początkowego prostoliniowego biegu torpedy oraz długości łuku torpedy, licząc od punktu zakończenia zwrotu A. Innymi słowy, długość odcinka E1A jest równa długości odcinka EA. Koncepcja idealnego punktu startu torpedy wynika z tego, że odległość pomiędzy nim a punktem zakończenia zwrotu torpedy jest równa odległości pomiędzy wyrzutnią torpedową a punktem zakończenia torpedy – co oznacza, że obydwa te odcinki zostaną przebyte przez torpedę w tym samym czasie. Położenie punktu E1 jest funkcją kąta odchylenia żyroskopowego ρ.
W ogólnym przypadku, kąt paralaksy δ jest funkcją trzech zmiennych: namiaru na cel ω, odległości do celu w chwili strzału E oraz kąta odchylenia żyroskopowego ρ:
δ = f(ρ, ω, E)
Do rozwiązania trójkąta torpedowego zbudowanego w oparciu o idealny punkt startu torpedy użyty jest kąt biegu γ (obserwowany z punktu idealnego startu torpedy), który jest kątem biegu γ1 (obserwowanym z miejsca lokalizacji celownika) zmodyfikowanym o wartość kąta paralaksy δ:
γ = γ1 + δ
Innymi słowy, kąt biegu γ to kąt biegu celu obserwowany z punktu idealnego startu torpedy, a różnica pomiędzy kątami biegu obserwowanymi z idealnego punktu startu torpedy oraz z miejsca lokalizacji celownika jest właśnie poprawką paralaksy.
Kąt paralaksy δ wprowadzany był do bloku rozwiązywania trójkąta torpedowego pośrednio.
Widoczny na wskaźniku zegarowym kąt biegu jest kątem γ1 (obserwowanym z miejsca lokalizacji celownika) i jest on ściśle powiązany z wartością kątów α i β (przy czym kąt β jest wyznaczany jako funkcja między innymi kąta α). Jak wspomniano wcześniej, jest on wyznaczany jako suma kąta strzału torpedowego β (który był wyznaczany jako funkcja między innymi kąta α) oraz kąta uderzenia torpedy α. Poprzez wprowadzenie dodatkowego składnika – kąta paralaksy δ – suma kątów będąca kątem biegu γ1 (obserwowanym z miejsca lokalizacji celownika) będzie zmieniona o wartość δ. Aby doprowadzić jego wartość do rzeczywistej wartości, operator poprzez niewielki obrót pokrętła odpowiedzialnego za wprowadzanie kąta uderzenia torpedy zmieniał wartość kąta strzału torpedowego β, który sumował się z kątem poprawki paralaksy δ oraz kątem uderzenia torpedy w cel α dając w rezultacie kąt biegu celu γ1 (obserwowany z miejsca lokalizacji celownika) – ale obliczony z uwzględnieniem poprawki paralaksy (poprzez zmianę kąta uderzenia w cel).
Rys. 10. Blok rozwiązywania trójkąta torpedowego z uwzględnieniem poprawki paralaksy [1]
Oczywiście, kąt poprawki paralaksy (jak wspomniano wcześniej) jest funkcją (między innymi) kąta odchylenia żyroskopowego ρ, który z kolei zależy od kąta strzału torpedowego β. W połączeniu z faktem, że do obliczenia kąta strzału torpedowego potrzebna jest znajomość kąta poprawki paralaksy, okazuje się, że do całościowego rozwiązania problemu należy rozwiązać układ dwóch równań (uwikłanych). Ten właśnie stosunkowo złożony problem obliczeniowy sprawił, że strzelanie torped z odchyleniem żyroskopowym stało się powszechne dopiero po opracowaniu odpowiednich urządzeń obliczeniowych (np. przez marynarki wojenne Niemiec, Japonii, Stanów Zjednoczonych). Natomiast w tych krajach, gdzie nie udało się opracować odpowiedniego kalkulatora (np. w Wielkiej Brytanii lub Polsce) - pomimo posiadania torped umożliwiających wykonanie zwrotu po opuszczeniu wyrzutni – strzelano torpedy na wprost – bez odchylenia żyroskopowego.
Obliczenie poprawki paralaksy δ odbywa się na podstawie znajomości położenia punktu idealnego startu torpedy. Współrzędne tego punktu (określone względem miejsca lokalizacji celownika torpedowego) w zależności od kąta odchylenia żyroskopowego ρ mogą być łatwo – przy znajomości długości początkowego prostoliniowego biegu torpedy, promienia skrętu (które dla torped G7a i G7e wynosiły odpowiednio 9,5 oraz 95 m) a także odległości pomiędzy wyrzutnią torpedową a miejscem lokalizacji celownika (w przypadku okrętów typu VIIC wynoszącej ~27 metrów) - analitycznie wyznaczone. Są one określone przy pomocy formuły (dla kąta odchylenia żyroskopowego z zakresu 0-90°):
x0 = 27 + 9,5 + 95 * sin ρ – (ρ * 95 + 9,5) * cos ρ
y0 = 95 * (1 - cos ρ) – (ρ * 95 + 9,5) * sin ρ
(wartość kąta nie będąca argumentem funkcji trygonometrycznych musi być podana w radianach)
Rys. 11. Położenie idealnego punktu strzału torpedy dla kąta odchylenia żyroskopowego ρ z zakresu 0-90°
Dla danej wartości kąta odchylenia żyroskopowego ρ, położenie idealnego punktu startu torpedy może zostać opisane względem miejsca lokalizacji celownika torpedowego przy użyciu współrzędnych biegunowych: X(ρ) – odległość pomiędzy miejscem lokalizacji celownika torpedowego a idealnym punktem startu torpedy, θ(ρ) – kąt pomiędzy diametralną okrętu a linią łączącą miejsce lokalizacji celownika torpedowego i idealny punkt startu torpedy.
Rys. 12. Współrzędne biegunowe idealnego punktu strzału torpedy
Współrzędne biegunowe X(ρ) oraz θ(ρ) mogą zostać wyrażone przy pomocy współrzędnych kartezjańskich:
\[\begin{aligned} X(ρ) = \sqrt[2]{{x_{0}}^2 + {y_{0}}^2} \end{aligned}\]
\[\begin{aligned} tg θ(ρ) = \frac{y_{0}}{x_{0}} \end{aligned}\]
czyli
\[\begin{aligned} θ(ρ) = arc tg\frac{y_{0}}{x_{0}} \end{aligned}\]
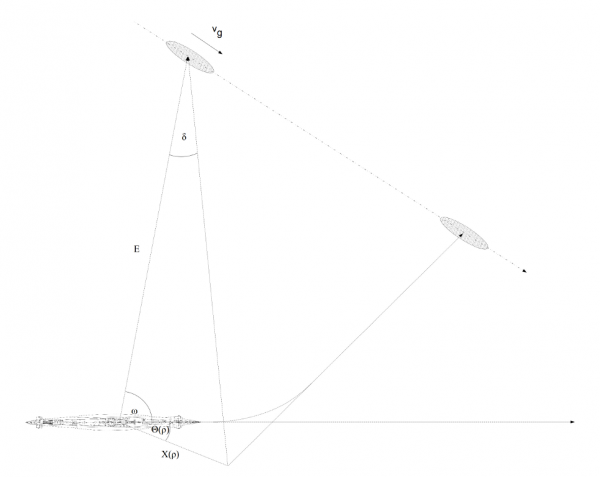
Stosując twierdzenie sinusów do trójkąta przedstawionego na poniższym rysunku otrzymujemy:
\[\begin{aligned} \frac{sin (ω + θ(ρ) + δ)}{E} = \frac{sin δ}{X(ρ)} \end{aligned}\]
gdzie E to odległość do celu w chwili strzału (mierzona z miejsca lokalizacji celownika torpedowego).
Rys. 13. Zależność pomiędzy poprawką paralaksy a położeniem punktu idealnego strzału torpedy
Powyższą zależność można przekształcić do postaci:
\[\begin{aligned} sin δ = X(ρ) * \frac{sin (ω + δ + θ(ρ))}{E} \end{aligned}\]
Ponieważ w praktyce wartość kąta paralaksy δ osiąga wartości maksymalnie 25°, można zastosować przybliżenie
\[\begin{aligned} sin δ = δ \end{aligned}\]
(dla kątów z zakresu 0 – 25°, sinus kąta równa się w przybliżeniu wartości kąta w mierze łukowej).
Zatem ostatecznie otrzymujemy:
\[\begin{aligned} δ = X(ρ) * \frac{sin (ω + δ + θ(ρ))}{E} \end{aligned}\]
Rozwiązanie tego równania uwikłanego realizuje blok obliczenia poprawki paralaksy.
 Rys. 14. Blok obliczania poprawki paralaksy [1]
Rys. 14. Blok obliczania poprawki paralaksy [1]
Z powyższego schematu wynika, że blok obliczania poprawki paralaksy zbudowany jest z jednej krzywki 2-wymiarowej, dwóch krzywek 3-wymiarowych, oraz z komparatora (sterującego silnikiem elektrycznym) zintegrowanego ze zespolonym wskaźnikiem zegarowym.
Dokładna, fizyczna implementacja bloku obliczania poprawki paralaksy nie jest znana, ale wydaje się, że krzywka 2-wymiarowa (której wartością wejściową jest kąt odchylenia żyroskopowego) jest krzywką podwójną, która generuje parę wartości wyjściowych - współrzędne biegunowe idealnego punktu startu torpedy (jej funkcjonalność można interpretować jako tablicę obliczonych wcześniej wartości).
Pierwsza, zaznaczona na rysunku krzywka 3-wymiarowa – w rzeczywistości prawdopodobnie jest zestawem dwóch krzywek 3-wymiarowych, z których jedna otrzymując jako wartości wejściowe wartości (ω + δ) oraz θ(ρ) generuje wartość sin (ω + δ + θ(ρ)), natomiast druga – otrzymując wartość wyjściową pierwszej krzywki oraz wartość X(ρ) realizuje funkcję:
\[\begin{aligned}g(ρ, ω + δ) = X(ρ) * sin (ω + δ + θ(ρ))\end{aligned}\]
Druga zaznaczona na rysunku krzywka 3-wymiarowa – otrzymując jako wartości wejściowe wartość generowaną przez pierwszą krzywkę 3-wymiarową oraz logarytm odległości do celu realizuje funkcję
\[\begin{aligned} h(g(ρ, ω + δ), E) = \frac{g(ρ, ω + δ)}{E}\end{aligned}\]
czyli
\[\begin{aligned} h(ρ, ω + δ, E) = X(ρ) * \frac{sin (ω + δ + θ(ρ))}{E}\end{aligned}\]
Wartość wyjściowa h(ρ, ω + δ, E) jest porównywana w komparatorze z wartością δ, wprowadzaną na pierwszą krzywkę 3-wymiarową – czyli realizowane jest równanie:
\[\begin{aligned} δ = X(ρ) * \frac{sin (ω + δ + θ(ρ))}{E} \end{aligned}\]
które posłużyło jako równanie wyjściowe do rozważań działania bloku obliczania poprawki paralaksy.
Sygnał błędu wytwarzany przez komparator steruje silnikiem elektrycznym, który obracając wałem odpowiadającym za wartość kąta paralaksy δ zmienia jego wartość. Układ w pętli sprzężenia zwrotnego dąży do zrównania lewej i prawej strony równania – prowadząc do jego rozwiązania.
Bieżąca wartość kąta z lewej i prawej strony równania jest wskazywana na zespolonym wskaźniku zegarowym (wskazówka obracający się na osi oraz wskazówka obracająca się wokół krawędzi tarczy).
W wypadku uszkodzenia systemu elektrycznego kalkulatora – dzięki ręcznemu pokrętłu sprzężonemu poprzez przekładnię różnicową z wałem reprezentującym wartość kąta paralaksy δ – możliwy jest ręczna obsługa urządzenia – operator obserwując wskazania na wskaźniku zegarowym, obracając pokrętłem stara się doprowadzić do zrównania wartości.
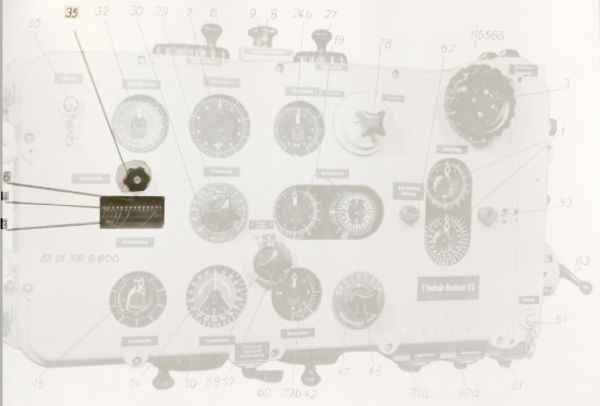
Fot. 8. Pokrętło (27) i wskaźnik zegarowy (24b) kąta paralaksy wraz z przełącznikiem paralaksy (28)
Fot. 9. Blok obliczania poprawki paralaksy
(24b) wskaźnik poprawki paralaksy, (25) silnik bloku obliczania poprawki paralaksy
Należy zwrócić uwagę, że jedną z wartości wejściowych drugiej krzywki 3-wymiarowej jest logarytm odległości do celu E. Występowanie w tym miejscu logarytmu jest efektem ubocznym uproszczenia układu w innymi miejscu kalkulatora - bloku obliczania kąta rozproszenia salwy torpedowej. Tam – zamiast wykonywania dzielenia dwóch wartości – zastosowano różnicę logarytmów. Dlatego też logarytm odległości jest doprowadzany także do bloku obliczenia poprawki paralaksy. Znów – nie jest do końca jasne jak to zaimplementowano – prawdopodobnie funkcja realizowana przez drugą krzywkę 3-wymiarową jest złożona także z funkcji wykładniczej (tzn. odwrotnej do funkcji logarytmicznej) w celu uzyskania odległości.
Dla dowolnych kątów odchylenia żyroskopowego wprowadzanych do torped rufowych wyrzutni torpedowych, kartezjańska współrzędna x0 idealnego punktu startu torpedy jest ujemna. Oznacza to, że współrzędna biegunowa θ(ρ) ma znak przeciwny w stosunku do wartości współrzędnej odpowiadającej kątom odchylenia żyroskopowego wprowadzonych do torped w dziobowych wyrzutniach torpedowych. Aby utrzymać poprawność obliczeń, należy w takim przypadku dokonać zmiany znaku wartości obliczanego kąta paralaksy δ na przeciwny. Odbywa się to przy pomocy dodatkowej pary przekładni 1:-1, włączanych do układu przełącznikiem paralaksy (Parallax Vorn/Acht). Przełącznik ten należy ustawić w odpowiedniej pozycji w zależności od tego, które wyrzutnie (dziobowe lub rufowe) mają zostać użyte do ataku.
Opis bloku obliczania kąta odchylenia żyroskopowego:
Obliczony w bloku rozwiązywania trójkąta torpedowego kąt strzału torpedowego β to kąt pomiędzy linią namiaru na cel w chwili strzału torpedy a torem torpedy. Aby wystrzelić torpedę według obliczonego kąta strzału, należało tak wycelować wyrzutnię (poprzez obrót aparatu torpedowego w przypadku wyrzutni obrotowych lub też poprzez celowanie całym okrętem w przypadku wyrzutni stałych), aby w chwili wystrzelenia torpedy kąt pomiędzy osią podłużną wyrzutni a linią namiaru na cel był równy kątowi strzału torpedy β. Wprowadzenie torped które miały możliwość wykonania – po opuszczeniu wyrzutni – zwrotu o nastawiony wcześniej kąt (kąt odchylenia żyroskopowego) zniosło konieczność celowania wyrzutnią bądź manewrowania okrętem.
Rys. 15. Trójkąt torpedowy dla strzału torpedowego bez odchylenia żyroskopowego oraz z odchyleniem żyroskopowym
Żyroskop torpedy należało wówczas nastawić na wykonanie zwrotu o kąt odchylenia żyroskopowego ρ, który jest równy sumie kąta strzału torpedowego β oraz namiaru na cel ω1 obserwowanego z punktu idealnego startu torpedy.
ρ = ω1 - β
Jak widać na poniższym rysunku, namiar na cel obserwowany z punktu idealnego startu torpedy jest równy namiarowy na cel obserwowanemu z miejsca lokalizacji celownika zmodyfikowanego o kąt paralaksy δ.
Rys. 16. Zależność pomiędzy namiarami na cel obserwowanymi z miejsca lokalizacji celownika torpedowego oraz z idealnego punktu strzału torpedy
Zatem kąt odchylenia żyroskopowego przyjmuje wartość równą:
ρ = ω + δ - β
Formuła ta realizowana jest przez blok obliczania kąta odchylenia żyroskopowego, który zbudowany jest z dwóch układów różnicowych dokonujących sumowania oraz podwójnego wskaźnika zegarowego połączonego z podwójnym nadajnikiem selsynowym.
Rys. 17. Blok obliczania kąta odchylenia żyroskopowego [1]
Wskaźnik zegarowy na dwóch tarczach – jedna o zakresie 0 - 360°, druga o zakresie 0 - 10° – wskazywał obliczoną wartość kąta odchylenia żyroskopowego. Kąt odchylenia żyroskopowego był wskazywany jako kąt kursowy względem diametralnej okrętu. Zintegrowane ze wskaźnikiem zegarowym nadajniki selsynowe przekazywały wartość kąta do odbiorników znajdujących się w przedziałach torpedowych.
Fot. 10. Podwójny wskaźnik kąta odchylenia żyroskopowego
Opis bloku obliczania maksymalnej odległości do celu w momencie odpalenia torpedy:
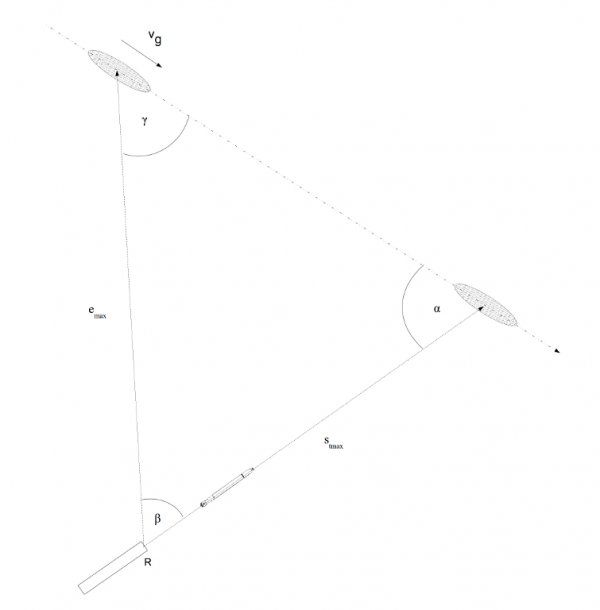
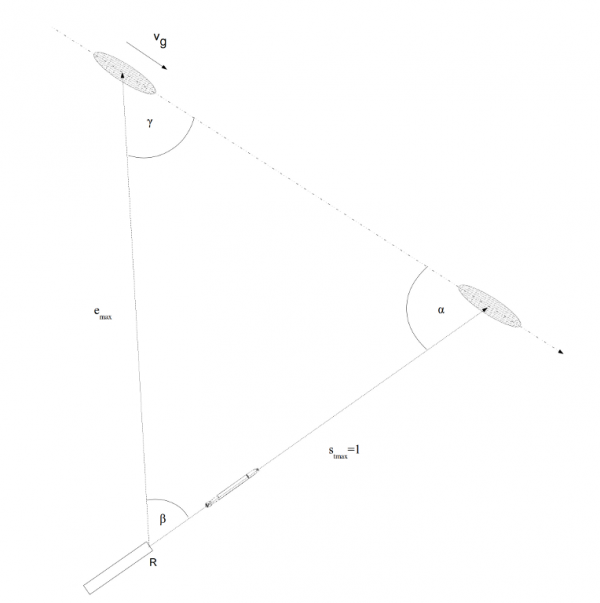
Blok rozwiązywania trójkąta strzału torpedowego umożliwiał także obliczenie największej dopuszczalnej odległości emax (niem. Reichentfernung) do celu w chwili strzału dla danego, maksymalnego zasięgu st max torpedy (niem. Reichweite).
Rys. 18. Trójkąt torpedowy zbudowany w oparciu o największą dopuszczalną odległość do celu emax oraz maksymalny zasięg torpedy st max
Dzięki temu, znając maksymalny zasięg torpedy, oficer torpedowy mógł się zorientować czy odległość w jakiej znajduje się cel w chwili strzału jest wystarczająca aby dosięgła go wystrzelona torpeda.
Fot. 11. Blok obliczania maksymalnej odległości do celu
(33) bęben obrazujący maksymalne zasięgi torped, (34) skala do odczytu największej dopuszczalnej odległości do celu w chwili strzału
Fot. 12. Wskaźniki i pokrętła bloku obliczania maksymalnej odległości do celu
(33) bęben obrazujący maksymalne zasięgi torped
(34) skala do odczytu największej dopuszczalnej odległości do celu w chwili strzału
(35) pokrętło maksymalnego zasięgu torpedy
(36) wskaźnik maksymalnego zasięgu torpedy
Wskaźnik maksymalnej odległości do celu zbudowany jest z obrotowego bębna (st max) o poziomej osi obrotu oraz nieruchomej, poziomej linijki (emax) z naniesioną skalą odległości w zakresie od 10 do 140 hm. Na bocznej powierzchni walca naniesione są linie oznaczone wartościami od 10 do 140 hm.
Ponadto, nad wskaźnikiem maksymalnej odległości do celu znajduje się pokrętło połączone z tarczą, umożliwiające wprowadzenie maksymalnego zasięgu torpedy (niem. Zulassige Schußweite, który dla torped parogazowych wynosił – w zależności od prędkości – 12500, 8000 i 6000 metrów, natomiast dla torped elektrycznych – w zależności od wersji – 5000 i 7500 metrów).
Fot. 13. Pokrętło maksymalnego zasięgu torpedy
W bloku rozwiązywania trójkąta torpedowego, oprócz obliczenia kąta strzału torpedy β wyznaczana jest odległość do celu dla jednostkowego zasięgu maksymalnego torpedy (czyli dla zasięgu maksymalnego torpedy równego 1).
Rys. 19. Trójkąt torpedowy zbudowany w oparciu o jednostkowy zasięg maksymalny torpedy st max= 1
Z powodu braku informacji na temat wewnętrznej budowy bloku rozwiązywania trójkąta torpedowego trudno jest z całą pewnością stwierdzić, w jaki sposób się to odbywało. Prawdopodobnie wykorzystano formułę (wykorzystując twierdzenie sinusów)
\[\begin{aligned} \frac{e}{sin α} = \frac{s_{t}}{sin (α + β)} \end{aligned}\]
czyli (dla jednostkowego st)
\[\begin{aligned} e = \frac{sin α}{sin (α + β)} \end{aligned}\]
Ta funkcja może być fizycznie zaimplementowana w postaci krzywki trójwymiarowej oraz układu różnicowego. Odległość do celu e (dla jednostkowego zasięgu maksymalnego torpedy) jest wyprowadzona na zewnątrz bloku przy użyciu wałka, który obracał bębnem.
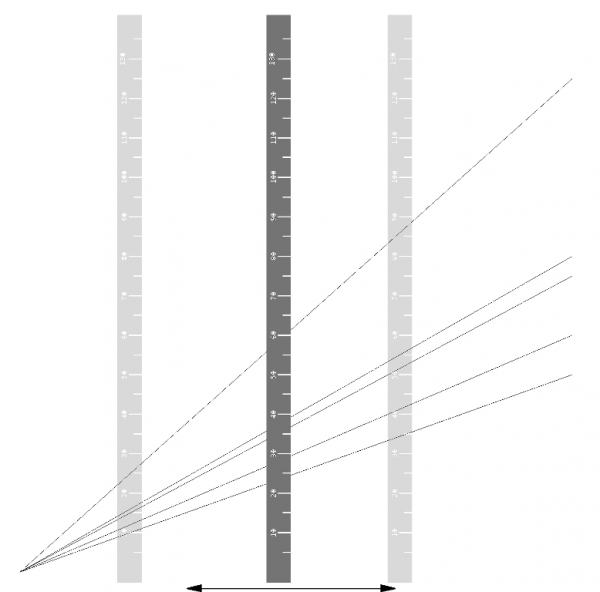
Na powierzchni bocznej bębna znajduje się szereg linii. Po rozwinięciu powierzchni bocznej bębna na płaszczyznę otrzymuje się poniższy rysunek.
Rys. 20. Bęben wskaźnika oraz rozwinięta powierzchnia boczna bębna
Po rozwinięciu powierzchni bocznej bębna – dla łatwiejszej interpretacji - można dokonać obrotu rysunku o 90°. Załóżmy teraz, że to nie bęben się obraca (czyli to nie powierzchnia boczna się przesuwa pod pionową linijką), ale to linijka przesuwa się w prawo lub w lewo.
Rys. 21. Rozwinięta powierzchnia boczna bębna po obróceniu o 90°
Ponieważ obrót walca – przesunięcie pionowej linijki – odpowiada odległości do celu e dla jednostkowego zasięgu torpedy st max = 1, to mnożąc tę odległość do celu przez dowolną wartość zasięgu torpedy (np. 5000 metrów) otrzyma się odległość do celu nie dla odległości jednostkowej, ale dla odległości równej przykładowo 5000 metrów. Można to formalnie zapisać:
emax = e * st max
gdzie st max przykładowo wynosi 5000 metrów.
Na powierzchni bocznej walca narysowane są linie, które są funkcjami liniowymi przedstawionymi przy pomocy powyższego równania dla różnych st max. Są to proste wychodzące z początku układu współrzędnych, różniące się jedynie nachyleniem. Zależność pomiędzy kątem nachylenia α a stałą st max jest następująca:
\[\begin{aligned}tg α = \frac{s_{t max}}{14000} \end{aligned}\]
Na poniższym rysunku wyróżniono (arbitralnie) jedną z linii na bocznej powierzchni walca, która odpowiada stałej równej st max = 7500 metrów. Odczyt szukanej wartości emax odbywa się poprzez znalezienie na ruchomej, pionowej linijce wartości która przecina się z daną linią odpowiadającą maksymalnemu zasięgowi torpedy. Szukana wartość na linijce odpowiada wartości funkcji
emax = e * st max
dla wartości odległości do celu e (dla jednostkowego zasięgu torpedy) obliczonego przez blok rozwiązywania trójkąta torpedowego oraz stałej st max odpowiadającej rzeczywistemu zasięgowi torpedy.
Rys. 22. Sposób odczytu maksymalnej odległości do celu w momencie strzału (wynoszącej w tym przypadku ~3650 metrów) dla torpedy o zasięgu 7500 metrów
Maksymalny zasięg torpedy jest ustawiany przy pomocy pokrętła na samym początku użycia kalkulatora. Pozwala to operatorowi w każdej chwili sprawdzić jego wartość (bez konieczności pamiętania tej wartości), odciążając go przy obsłudze urządzenia. W przypadku użycia kalkulatora do strzelania salwą torped o różnego typu (np. salwa dwóch torped parogazowych oraz dwóch torped elektrycznych), wprowadzana jest wartość równa mniejszemu z zasięgów użytych torped.
Rys. 23. Blok obliczania maksymalnej odległości do celu w momencie odpalenia torpedy [1]
Opis bloku obliczania kąta rozproszenia salwy torpedowej:
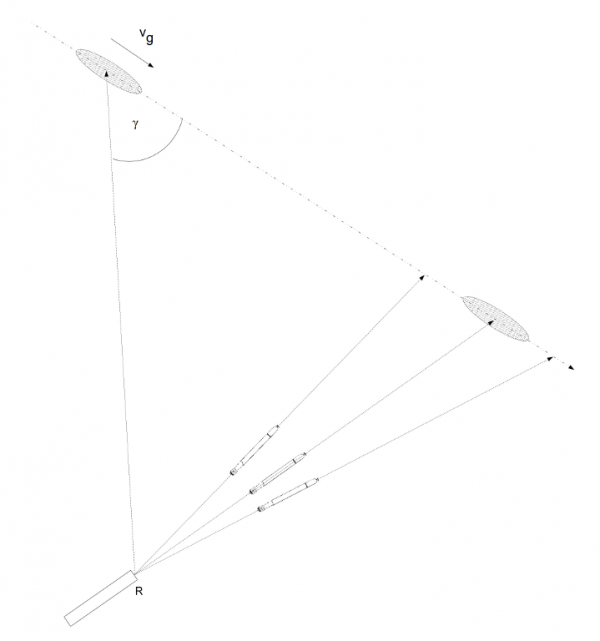
W przypadku strzelania salwą, każda z torped biegnie nieco innym kursem. Zwiększa to prawdopodobieństwo trafienia celu, ponieważ kilka torped przecina kurs celu w kilku punktach (pozwalając na margines błędu w określeniu parametrów ruchu celu), a nie tylko w jednym punkcie – jak ma to miejsce w przypadku strzału pojedynczego.
Rys. 24. Salwa torpedowa
Kąt odchylenia żyroskopowego ρ torped w salwie torpedowej jest obliczany identycznie jak w przypadku pojedynczego strzału torpedowego, jednak dodatkowo kalkulator oblicza także kąt rozproszenia salwy torpedowej ψ – czyli wartość, o jaką należy zmodyfikować kąt odchylenia żyroskopowego. Obydwie te wartości: kąt odchylenia żyroskopowego ρ oraz kąt rozproszenia salwy torpedowej ψ są przesyłane łączami selsynowymi do odbiornika kąta odchylenia żyroskopowego (niem. Schußwinkelempfänger). W odbiorniku kąta odchylenia żyroskopowego, w zależności od wybranej liczebności salwy torpedowej, następowało właściwe wyznaczenie kąta odchylenia żyroskopowego dla poszczególnych torped salwy. Opis działania odbiornika kąta odchylenia żyroskopowego znajduje się tutaj.
Kąt rozproszenia salwy torpedowej ψ zależy od odległości do celu E, długości celu l, kąta biegu γ oraz stosunku prędkości celu i torpedy \(\frac{v_{g}}{v_{t}}\).
Kąt rozproszenia salwy torpedowej obliczany jest w następujący sposób. Poniższy rysunek przedstawia tor biegu torpedy, kurs celu oraz linię namiaru na cel w momencie strzału. Rysunek jest tak zorientowany, że linia namiaru na cel pokrywa się z poziomą osią układu współrzędnych.
Rys. 25. Trójkąt torpedowy
Współrzędne położenia torpedy T oraz celu Z w zależności od czasu przedstawić można przy pomocy par równań:
T: \( \begin{cases} x = t * v_{t} * cos β \\ y = t * v_{t} * sin β \end{cases} \) Z: \( \begin{cases} x = E – t * v_{g} * cos γ \\ y = t * v_{g} * sin γ \end{cases} \)
gdzie t – czas, vt – prędkość torpedy, vg – prędkość celu, β – kąt strzału torpedowego, γ – kąt biegu, E – odległość do celu w momencie strzału.
Współrzędne położenia punktu z odległego od punktu Z o odległość λ (na kursie celu) można przedstawić następująco:
z: \( \begin{cases}x = E – (t * v_{g} + λ) * cos γ \\ y = (t * v_{g} + λ) * sin γ\end{cases} \)
Rys. 26. Trójkąt torpedowy wraz z przedstawionym punktem z
Współrzędne dziobu oraz rufy celu można zatem zdefiniować używając pary wartości λ = λ0 i λ = -λ1.
Kwadrat odległości pomiędzy punktem, w którym znajduje się torpeda T a punktem z może zostać przedstawiony zależnością:
\[\begin{aligned}|Tz|^{2} = (x_{T} – x_{z})^{2} + (y_{T} – y_{z})^{2} \end{aligned}\]
Aby torpeda przeszła przez punkt z (czyli trafiła w dziób lub rufę celu), odległość |Tz| musi wynosić 0 czyli:
\[\begin{aligned}0 = (x_{T} – x_{z})^{2} + (y_{T} – y_{z})^{2}\end{aligned}\]
Ten warunek może być spełniony jedynie wtedy, gdy jednocześnie zachodzi:
\((x_{T} – x_{z})^{2} = 0\) i \((y_{T} – y_{z})^{2} = 0 \)
czyli
\[\begin{aligned}(t * v_{t} * cos β – E + (t * v_{g} + λ) * cos γ)^{2} = 0 \end{aligned}\]
i
\[\begin{aligned}(t * v_{t} * sin β – (t * v_{g} + λ) * sin γ)^2 = 0 \end{aligned}\]
Z powyższych równań można wyznaczyć wartość t:
\[\begin{aligned}t = \frac{E - λ * cos γ}{v_{t} * cos β + v_{g} * cos γ}\end{aligned}\]
i
\[\begin{aligned}t = \frac{λ * sin γ}{v_{t} * sin β – v_{g} * sin γ}\end{aligned}\]
a następnie przyrównać do siebie:
\[\begin{aligned}\frac{E - λ * cos γ}{v_{t} * cos β + v_{g} * cos γ} = \frac{λ * sin γ}{v_{t} * sin β – v_{g} * sin γ}\end{aligned}\]
Wykonując następujące podstawienie:
\(u = \frac{v_{g}}{v_{t}}\) oraz \(μ = \frac{λ}{E}\)
otrzymujemy:
\[\begin{aligned}sin β – u * sin γ = μ * sin (β + γ) \end{aligned}\]
Jest to uwikłane równanie, które pozwala wyznaczyć kąt strzału torpedowego β dla celu widzianego pod kątem biegu γ, tak aby torpeda trafiła w punkt z leżący w odległości λ od środka celu.
Rys. 27. Trójkąt torpedowy z torpedą trafiającą w punkt z
Należy zwrócić uwagę, że dla λ równej 0 (czyli dla przypadku gdy chcemy aby torpeda trafiła w sam środek celu), równanie to przyjmuje postać:
\[\begin{aligned}sin β – u * sin γ = 0\end{aligned}\]
Pamiętając, że
\[\begin{aligned}u = \frac{v_{g}}{v_{t}}\end{aligned}\]
widzimy, że jest to twierdzenie sinusów zastosowane do trójkąta torpedowego.
Dla wygody, zamiast rozpatrywać położenie rufy oraz dziobu celu jako odległości λ od środka celu, można wprowadzić następujące podstawienie:
\[\begin{aligned}μ_{0} = \frac{l}{2*E}\end{aligned}\]
gdzie l – długość celu.
Czyli aby trójtorpedowa salwa trafiła odpowiednio w dziób, środek oraz rufę celu, każda z trzech torped musi zostać wystrzelona pod kątem odpowiednio β0, β i β1, gdzie każda z tych wartości spełnia jedno z następujących równań:
\[\begin{cases}sin β_{0} – u * sin γ = μ_{0} * sin (β_{0} + γ) \\ sin β – u * sin γ = 0 \\ sin β_{1} – u * sin γ = - μ_{0} * sin (β_{1} + γ)\end{cases}\]
Rys. 28. Trójkąt torpedowy dla salwy torpedowej
Ponieważ w praktyce, w większości przypadków cel o długości do około 150 metrów (np. statki typu Liberty ~135 m, tankowce typu T2 ~152 m) jest atakowany z odległości minimum 500 metrów, to wartość μ0 jest niewielka (μ0 < 0,15). Oznacza to, że kąt pomiędzy kursami torped trafiających w dziób i rufę celu (tzn. β1 - β0 ) wynosi maksymalnie ~20°. Wykorzystując fakt, że dla kąta α z zakresu 0 – 20°, sin α ~ α oraz cos α ~ 1, powyższe trzy równania można przekształcić do postaci:
\[\begin{cases}sin β – u * sin γ = μ_{0} * sin (β + γ) – (β_{0} - β) * cos β \\ sin β – u * sin γ = 0 \\ sin β – u * sin γ = - μ_{0} * sin (β + γ) – (β_{1} - β) * cos β\end{cases}\]
Wstawiając środkowe równanie do dwóch pozostałych równań otrzymujemy dwa równania:
\[\begin{cases}β_{0} - β = \frac{μ_{0} * sin (β + γ)}{cos β} \\ β_{1} - β = - \frac{μ_{0} * sin (β + γ)}{cos β}\end{cases}\]
Zatem kąt rozproszenia salwy torpedowej ψ (będący różnicą kątów β1 – β0) można obliczyć przy użyciu następującej formuły:
\[\begin{aligned}ψ = \frac{2 * μ_{0} * sin (β + γ)}{cos β}\end{aligned}\]
Formułę tę można przekształcić do postaci:
\[\begin{aligned}ψ = \frac{l}{E} * sin γ * (1 + \frac{cos γ}{\sqrt[2]{\frac{v_{t}}{v_{g}}^{2}-sin^{2}γ}})\end{aligned}\]
w której wartość kąta rozproszenia salwy torpedowej zależy od kąta biegu γ, długości celu l, odległości do niego w chwili strzału E oraz ilorazu prędkości torpedy oraz celu \(\frac{v_{t}}{v_{g}}\).
Ta formuła jest dużo bardziej złożona pod względem obliczeniowym, ma jednak tę zaletę, że nie użyto w niej wartości będących wynikiem obliczeń innych bloków kalkulatora (kąta strzału torpedy β). Prawdopodobnie projektanci kalkulatora chcieli w ten sposób zapewnić funkcjonalność obliczania kąta strzału torpedowego nawet w wypadku uszkodzenia bloku rozwiązywania trójkąta torpedowego.
Formuła ta została zaimplementowana w kalkulatorze przy użyciu dwóch krzywek trójwymiarowych oraz układów różnicowych.
 Rys. 29. Blok obliczania kąta rozproszenia salwy torpedowej [1]
Rys. 29. Blok obliczania kąta rozproszenia salwy torpedowej [1]
Pierwsza z dwóch krzywek trójwymiarowych otrzymuje na swoje wejście iloraz prędkości celu oraz torpedy \(\frac{v_{g}}{v_{t}}\) oraz kąt biegu γ.
Jak wspomniano wcześniej (przy opisie bloku obliczania poprawki paralaksy), odległość do celu wprowadzana była w postaci logarytmicznej. W podobny sposób wprowadzana jest długość celu. Dzięki temu, obliczenie ilorazu \(\frac{l}{E}\) sprowadza się do wykonania odejmowania w układzie różnicowym. Logarytm tego ilorazu jest doprowadzany (wraz z wartością wyjściową pierwszej krzywki trójwymiarowej) na wejście drugiej krzywki trójwymiarowej. Jej wartością wyjściową jest szukany kąt rozproszenia salwy torpedowej ψ.
Wartość kąta rozproszenia salwy torpedowej jest wyświetlana na wskaźniku zegarowym, o zakresie od 0 do 20°. Wskaźnik ten jest wskaźnikiem zespolonym – jego wewnętrzna wskazówka wskazuje obliczony kąt, natomiast wskazówka zewnętrzna (na krawędzi tarczy) wskazuje położenie wału obracanego przez silnik elektryczny. Silnik elektryczny jest sterowany sygnałem błędu wynikającym z różnicy wzajemnego położenia wskazówek – tzn. silnik elektryczny będzie obracał wałem tak, aby wskazówki wskazywały tę samą wartość. Wał obracany przez silnik napędza także nadajnik selsynowy, który przekazuje wartość kąta do odbiornika kąta odchylenia żyroskopowego.
W przypadku awarii systemu elektrycznego lub uszkodzenia silnika elektrycznego, możliwy jest ręczny napęd wału (poprzez przekładnię różnicową) przy pomocy dedykowanego pokrętła.
Ponadto – po wyłączeniu silnika elektrycznego – możliwe jest ręczne wprowadzenie arbitralnego kąta rozproszenia salwy torpedowej przy pomocy pokrętła.
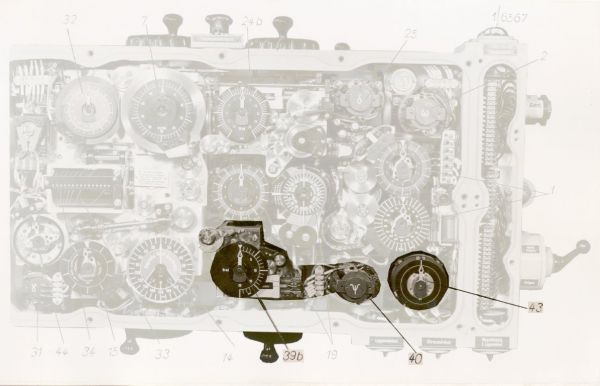
Fot. 14. Blok obliczania kąta rozproszenia salwy torpedowej
(39b) wskaźnik kąta rozproszenia salwy torpedowej
(40) silnik bloku obliczania kąta rozproszenia salwy torpedowej
(43) nadajnik selsynowy kąta rozproszenia salwy torpedowej
Fot. 15. Wskaźniki i pokrętła bloku obliczania kąta rozproszenia salwy torpedowej
(39b) wskaźnik rozproszenia salwy torpedowej
(42) pokrętło rozproszenia salwy torpedowej
(57) pokrętło długości celu
(58) wskaźnik długości celu
Z wałem silnika elektrycznego sprzęgnięty jest także tzw. „wskaźnik położenia zerowego”. W zależności od położenia przełącznika rodzaju salwy torpedowej (Einzelnschuß - na skrzynce sterującej systemu odpalania torped), silnik jest sterowany poprzez wskaźnik kąta rozproszenia salwy torpedowej (w przypadku ustawienia strzału salwą) lub też poprzez wskaźnik położenia zerowego (w przypadku strzału pojedynczego). W tym drugim przypadku, silnik elektryczny będzie starał utrzymać się wał w położeniu zerowym (niezależnie od wyliczonego kąta rozproszenia salwy torpedowej), dzięki czemu w przypadku strzału pojedynczego, do odbiornika kąta odchylenia żyroskopowego przesyłana będzie wartość ψ = 0.
Rys. 30. Blok obliczania kąta rozproszenia salwy torpedowej – wskaźnik położenia zerowego [1]
Należy zaznaczyć, że blok obliczania kąta rozproszenia salwy torpedowej wyznacza kąt ψ pomiędzy kursami torped, które trafiają w dziób i rufę celu. Rzeczywisty kąt rozproszenia salwy torpedowej (kąt pomiędzy kursami dwóch skrajnych torped w salwie) zależy od liczebności salwy i jest wyznaczany w odbiorniku kąta odchylenia żyroskopowego.
Uzupełnieniem bloku obliczania kąta rozproszenia salwy torpedowej jest wskaźnik maksymalnego odchylenia salwy. Wskaźnik ten został wprowadzony ponieważ niemieckie torpedy mogły wykonać zwrot o maksymalnej wartości równej 90°. Możliwe były sytuacje, gdy obliczony kąt odchylenia żyroskopowego torpedy był bliski tej wartości (wynosząc np. 85°), natomiast kąt rozproszenia salwy czterotorpedowej wynosił (przykładowo) 10°. W takiej sytuacji kąty odchylenia żyroskopowego dla poszczególnych torped wynosiłyby: 100°, 90°, 80° i 70° – czyli kąt ten dla jednej torpedy przekraczałby dopuszczalną wartość. Aby sygnalizować takie sytuacje, wprowadzono wskaźniki maksymalnego odchylenia salwy torpedowej w postaci trzech par ruchomych przesłon, znajdujących się na zewnętrznej krawędzi wskaźnika odchylenia żyroskopowego.
Fot. 16. Wskaźniki maksymalnego odchylenia salwy torpedowej
Pary tych przesłon poruszały się niezależnie, proporcjonalnie do wartości 1,5ψ, ψ i 0,5ψ – zbliżając się i oddalając od wskaźnika zerowego. Kąt odchylenia żyroskopowego był wskazywany przez nieruchomy wskaźnik zerowy na obracającej się tarczy wyskalowanej w zakresie od 0 do 360°. Na tarczy tej znajdowała się poprzeczka przechodząca przez środek tarczy oraz wartości kąta 90° i 270° – wskazująca maksymalny kąt odchylenia żyroskopowego torped. Rozsuwające się przesłony odsłaniały czerwone tło znajdujące się pod nimi. Gdy poprzeczka na tarczy wskaźnika znalazła się na czerwonym tle, oznaczało to, że salwa torpedowa wykracza poza dopuszczalny zakres nastaw kątów odchylenia żyroskopowego i należy zmienić parametry ataku.
Rys. 31. Wskaźniki maksymalnego odchylenia salwy torpedowej dla różnych wartości kąta rozproszenia salwy torpedowej oraz odchylenia żyroskopowego
Opis bloku wprowadzania kąta namiaru na cel:
Kąt namiaru na cel ω – używany do obliczeń kąta poprawki paralaksy oraz kąta odchylenia żyroskopowego – jest przekazywany do kalkulatora przy pomocy łącza selsynowego. Podwójny odbiornik selsynowy otrzymywał wskazania z jednego z trzech nadajników namiaru (Ziel-Geber - celownika nocnego UZO na pomoście, peryskopu bojowego w kiosku oraz peryskopu nocnego w centrali), wybranego przy pomocy przełącznika systemu celowania (Zielrichtung). Z odbiornikiem zintegrowany był podwójny, zespolony wskaźnik zegarowy posiadający dwie tarcze zegarowe – jedna o zakresie 0 - 360°, druga o zakresie 0 – 10°.
Fot. 17. Blok wprowadzania kąta namiaru na cel
(1) wskaźnik kąta namiaru na cel
(2) silnik bloku wprowadzania kąta namiaru na cel
Każda z tarcz posiadała dwie wskazówki - pierwsza z nich obracając się na osi w środku tarczy wskazywała wartość otrzymaną przez odbiornik selsynowy, druga z nich – obracając się wokół krawędzi tarczy – bieżącą nastawę wprowadzoną do kalkulatora. Różnica w położeniu tych wskazówek wytwarzała sygnał błędu sterujący silnikiem elektrycznym, który obracając wałkiem przekazywał wartość kąta namiaru na cel do dalszych części kalkulatora (ponieważ odbiornik selsynowy miał zbyt małą moc na swoim wale wyjściowym, aby poruszać pozostałe mechanizmy kalkulatora).
Rys. 32. Blok wprowadzania kąta namiaru na cel [1]
Pomiędzy zespolonym wskaźnikiem zegarowym a silnikiem znajdował się przekaźnik, który był sterowany przy pomocy przełącznika śledzenia celu (Blauschalter). W położeniu spoczynkowym, przekaźnik rozłączał połączenie pomiędzy wskaźnikiem a silnikiem elektrycznym – bieżący namiar peryskopu/celownika nocnego nie wpływał na nastawy kalkulatora. Gdy padał rozkaz „Namiar na bieżąco” (Folgen!) - włączano przełącznik śledzenia celu a przekaźnik łączył wskaźnik zespolony z silnikiem elektrycznym, dzięki czemu bieżący namiar peryskopu/celownika nocnego był przekazywany do mechanizmów kalkulatora. Rozwiązanie takie umożliwiało aktualizowanie namiaru na celu (w położeniu Folgen!), natomiast gdy zachodziła potrzeba obejrzenia horyzontu – aby nie zmieniać prawidłowych nastaw kalkulatora wydawano rozkaz „Wyłączyć namiar na bieżąco!” (Blau! Nicht folgen!) - co prowadziło do odłączenia silnika elektrycznego od zespolonego wskaźnika zegarowego.
Na wypadek awarii silnika elektrycznego lub też systemu przekazywania namiaru z nadajników namiaru – kalkulator był wyposażony w pokrętło ręcznego wprowadzania namiaru, które poprzez przekładnię różnicową obracało wałem przekazującym wartość namiaru do dalszych części kalkulatora. Operator kalkulatora ręcznie ustawiał wartość namiaru na cel przekazaną ustnie od oficera torpedowego (w przypadku awarii systemu przekazywania namiaru z nadajników namiaru) lub też doprowadzał do zrównania wartości wskazywanych przez obydwie wskazówki wskaźnika zespolonego (w przypadku awarii silnika elektrycznego).
Fot. 18. Wskaźnik (1) namiaru na cel wraz z pokrętłem (3) ręcznego wprowadzania namiaru
Blok wprowadzania kąta namiaru na cel umożliwiał także wprowadzenie poprawki na prędkość kątową zwrotu wykonywanego przez okręt w trakcie strzelania torped. Poprawka ta była związana z czasem rozruchu żyroskopów niemieckich torped który określono na tv = 0,4 s. W tym czasie żyroskopy były zablokowane. Oznaczało to, że w przypadku wykonywania zwrotu przez okręt, w trakcie którego strzelano torpedy, oś podłużna opuszczającej wyrzutnię torpedy (wraz zablokowanym żyroskopem) obróciła się o kąt \(t_{v}*\frac{φ}{t}\), gdzie \(\frac{φ}{t}\) jest to prędkość kątowa zwrotu okrętu, zależna od prędkości okrętu oraz stopnia wychylenia steru.
|
prędkość [węzły] |
30° | 15° | |
| ↑ |
17,5 | 2,5 | 1,8 |
| 12 | 1,7 | 1,25 | |
| ↓ | 8 | 1,4 | 1,0 |
| 4,5 | 0,85 | 0,6 |
Prędkość kątowa zwrotu jest uwzględniona poprzez poprzez dodanie do wartości namiaru celu wprowadzonej przy pomocy pokrętła poprawki. Namiar na cel wyświetlany na wskaźniku był rzeczywistym namiarem na cel, jednak nastawa namiaru przekazywana do dalszych bloków kalkulatora była zmodyfikowana o wprowadzoną poprawkę prędkości kątowej zwrotu.
Fot. 19. Pokrętło (48) oraz wskaźnik (47) poprawki na prędkość kątową zwrotu
Opis bloku obliczania bieżącego kąta biegu:
Gdy cel oraz własny okręt płyną stałym kursem, wówczas zmiany namiarów na cel są równe zmianie kątów biegu celu.
Rys. 33. Zmiana namiaru oraz kąta biegu celu przy stałym kursie własnym
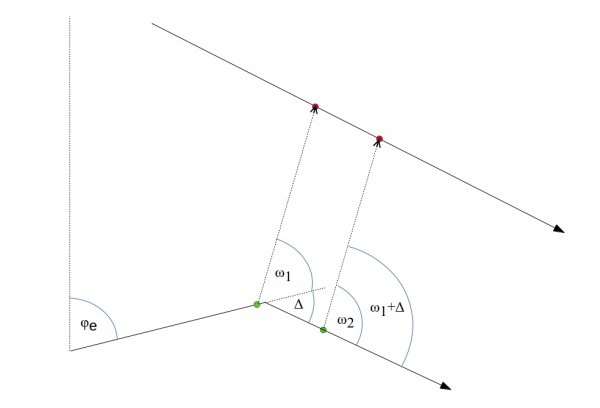
Innymi słowy, różnica kątów biegu oraz namiarów na cel w dwóch różnych momentach była taka sama:
Δ = ω1 – ω2 i Δ = γ1 – γ2
Można to przekształcić do postaci:
ω1 – ω2 = γ1 – γ2
czyli:
ω1 – γ1 = ω2 – γ2
Zatem w dowolnym momencie (zakładając stały kurs własnego okrętu oraz stały kurs celu), różnica namiaru na cel oraz kąta biegu jest stała.
Wykorzystując tę regułę, kalkulator torpedowy wyposażono w blok obliczający bieżący kąt biegu, który uaktualniał wprowadzony wstępnie kąt biegu.
Rys. 34. Blok obliczania bieżącego kąta biegu [1]
Blok ten zbudowany był z odbiornika selsynowego, który odbierał z żyrokompasu wskazania kursu własnego okrętu φe. Wartość kursu była podawana na jedno z dwóch wejść układu porównującego. Na drugie wejście tego układu była podawana różnica wartości kąta biegu γ oraz kąta namiaru na cel ω. Gdy wartość namiaru na cel (w wyniku poruszania się celu) zmieniała się, zmianie ulegała różnica namiaru i kąta biegu. Zmiana tej różnicy była porównywana z niezmiennym kursem własnym i generowała sygnał sterujący silnikiem elektrycznym, który przez przekładnię różnicową zmieniał kąt biegu w taki sposób, aby przywrócić poprzednią wartość różnicy namiaru na cel i kąta biegu.
Pomiędzy odbiornikiem selsynowym kursu φe a komparatorem znajdowało się sprzęgło elektromagnetyczne, sterowane przełącznikiem „Kąt biegu na bieżąco” (Lage laufend). Gdy sprzęgło było włączone, wartość kursu była przekazywana do komparatora a cały blok automatycznie uaktualniał bieżący kąt biegu. Gdy sprzęgło było wyłączone, wówczas wartość kursu nie była przekazywana do komparatora. Wówczas można było dokonać ręcznej poprawki kąta biegu przy pomocy pokrętła. W takiej sytuacji – wskutek wyłączonego sprzęgła – wał wejściowy komparatora reprezentujący kurs mógł się obracać swobodnie. Ponieważ wały wejściowe w komparatorze były sprzęgnięte ze sobą poprzez przekładnię różnicową, nieobciążony wał reprezentujący kurs obracał się o taką samą wartość jak wał reprezentujący różnicę kąta biegu oraz namiaru na cel. Dlatego pomimo zmieniającej się różnicy kąta biegu oraz namiaru na cel (wskutek ręcznej zmiany kąta biegu) sygnał błędu komparatora był równy zero – silnik elektryczny uaktualniający kąt biegu był wyłączony. Po zakończeniu wprowadzania ręcznych poprawek kąta biegu, przełącznik „Kąt biegu na bieżąco” ponownie włączał sprzęgło, sprzęgając odbiornik selsynowy z komparatorem.
Należy zwrócić uwagę, że blok obliczania bieżącego kąta biegu kompensował także zmiany namiaru na cel wynikające ze zmiany kursu własnego.
Jeżeli kurs własny φe zmienił się o wartość Δ, oznacza to, że namiar na cel również zmienił się o tę samą wartość.
Rys. 35. Zmiana namiaru podczas zmianie kursu własnego
Oznacza to, że obydwie porównywane wartości przekazywane do komparatora (różnica ω – γ oraz φe) zmieniły się o tę samą wartość – sygnał błędu komparatora był równy zero – silnik elektryczny uaktualniający kąt biegu był wyłączony – kąt biegu pozostawał niezmienny pomimo zmiany namiaru na cel. Z komparatorem zintegrowany był wskaźnik zegarowy, który posiadał skalę w zakresie od 0 do 10°. Służył on do wskazywania względnej zmiany własnego okrętu.
Fot. 20. Blok obliczania bieżącego kąta biegu
(15) wskaźnik zmiany kursu własnego, (31) silnik bloku obliczania bieżącego kąta biegu
Należy zwrócić uwagę, że w kalkulatorze torpedowym pochodzącym z U 955, tarcza tego wskaźnika ma zakres całkowity 60 i jest opisana jako "Vorlf. sek." czyli "czas początkowego biegu (torpedy)". Spowodowane to jest najprawdopodobniej tym, że w trakcie prac renowacyjnych, oryginalna tarcza została wymieniona na tarczę zastępczą, nie troszcząc się o wierność w stosunku do oryginału. Ten wskaźnik w żaden sposób nie był związany z jakimkolwiek czasem.
Opis bloku obliczania bieżącego namiaru na cel:
W przypadku strzelania salwą, torpedy są odpalane kolejno w odstępach wynoszących około 2,3 sekundy. Wystrzelenie pełnej salwy czterotorpedowej (lub nawet sześciotorpedowej w przypadku okrętów typu XXI) trwałoby zatem od 9 do 14 sekund. Przez cały ten czas, aby utrzymać poprawność wyliczenia kąta odchylenia żyroskopowego (który jest między innymi sumą kata namiaru na cel) należałoby utrzymywać peryskop/celownik nocny UZO cały czas nakierowany na cel. Oficer torpedowy musiałby być cały czas skupiony na celowaniu - ze względów taktycznych nie jest to pożądane. Dlatego kalkulator torpedowy wyposażony został także w blok obliczania bieżącego namiaru na cel.
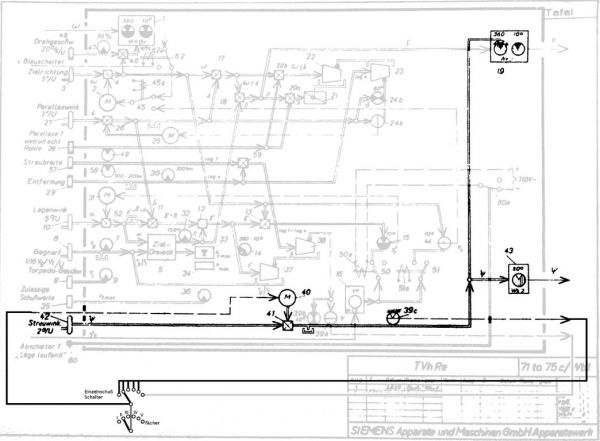
Rys. 36. Blok obliczania bieżącego namiaru na cel [1]
Blok ten zbudowany jest z komparatora, którego jedno wejście jest połączone – poprzez sprzęgło elektromagnetyczne – z wyjściem odbiornika selsynowego kursu własnego okrętu. Na drugie wejście komparatora jest podawany kąt namiaru na cel. Sygnał wyjściowy komparatora może być podłączony – za pośrednictwem przekaźnika – do silnika elektrycznego wprowadzającego namiar celu do kalkulatora.
Sprzęgło elektromagnetyczne oraz przekaźnik są włączane w momencie naciśnięcia dźwigni spustowej (Abfeuerschalter) – w momencie odpalenia pierwszej torpedy w salwie. Gdy przełącznik systemu odpalania (Einzelnschuß) jest w pozycji „strzał pojedynczy” - sterowanie sprzęgłem oraz przekaźnikiem jest odłączone.
Rys. 37. Sterowanie bloku obliczania bieżącego namiaru na cel [1]
W momencie naciśnięcia dźwigni spustowej (odpalenia pierwszej torpedy), sprzęgło elektromagnetyczne łączy komparator z odbiornikiem selsynowym kursu własnego, natomiast sygnał wyjściowy komparatora jest podłączany do silnika elektrycznego wprowadzającego namiar celu zamiast sygnału z odbiornika kąta namiaru celu. Oznacza to, że od tego momentu obrót peryskopu lub celownika nocnego UZO nie ma wpływu na namiar celu wprowadzony do kalkulatora. Ponadto, okręt może w trakcie strzelania salwy wykonywać zwrot – zmiana namiaru na cel wynikająca ze zmiany kursu własnego okrętu jest kompensowana – kąt odchylenia żyroskopowego będzie uaktualniany na bieżąco. Ponieważ w układzie nie zastosowano przekaźnika podtrzymującego, dźwignia spustowa musi być naciskana do momentu odpalenia ostatniej torpedy w salwie (jest to sygnalizowane na tablicy lampek kontrolnych odpalania torped).
Fot. 21. Blok obliczania bieżącego namiaru na cel
(2) silnik bloku wprowadzania namiaru na cel
(44) komparator bloku obliczania bieżącego namiaru na cel
Źródła:
[1] Die Torpedos der deutschen U-Boote, Eberhard Rössler